Artikel und Medien

Bei der Entwicklung von Aufgaben im Antwort-Wahl-Verfahren handelt es sich um eine sehr anspruchsvolle Tätigkeit. Es gilt daher einiges zu beachten, damit eine hinreichende Aufgabenqualität erreicht wird. Aus diesem Grund haben mehrere Autor(/-inn)en Item-Guidelines entwickelt, die zur Unterstützung bei der Fragenentwicklung hinzugezogen werden können (z.B. in Brauns & Schubert, 2008). Einige der in diesen Guidelines genannten Gestaltungsregeln werden im Folgenden genauer erläutert:

Grundsätzlich gilt, dass jede der Aufgaben im Antwort-Wahl-Verfahren der Überprüfung eines spezifischen Inhalts dient (Brauns & Schubert, 2008). Idealerweise orientieren sich die Fragen daher an den Zielen der Lehrveranstaltung und bilden diese repräsentativ in der Klausur ab (Biggs & Tang, 2011). Für die Klausur als Ganzes ist dabei darauf zu achten, dass die einzelnen Fragen voneinander unabhängig bleiben, damit eine vorherige Aufgabe keine Lösungshinweise für eine nachfolgende Aufgabe liefert (Brauns & Schubert, 2008).

Eine notwendige Voraussetzung für eine ökonomische Wissenserfassung besteht in der Minimierung des Leseaufwands (Lindner et al., 2015). Daher muss bei der Formulierung des Fragefelds und der Antworten darauf geachtet werden, den Textumfang gering zu halten (Brauns & Schubert, 2008). Auch das Vokabular und die Grammatik sollten so einfach wie möglich sein (ebenda). Bei der Erstellung des Fragefelds sollten Sie ferner darauf achten, dass die Aussage in positiver Richtung und die Frage so kurz wie möglich, aber trotzdem ausführlich genug und klar verständlich formuliert ist (ebenda) Das bedeutet, dass doppelte Verneinungen genauso zu vermeiden sind wie Abkürzungen, es sei denn, sie können als bekannt vorausgesetzt werden. Generell sind nur Begriffe, Metaphern und Vergleiche empfehlenswert, die als bekannt vorausgesetzt werden können. Negationen sollten immer auf die gleiche Art und Weise hervorgehoben sein.

Um Aufgaben im Antwort-Wahl-Verfahren auf unterschiedlichen kognitiven Anspruchsniveaus zu generieren, kann es hilfreich sein, mit den Stufen der kognitiven Lernzieltaxonomie (Anderson & Krathwohl, 2001) korrespondierende Frageanfänge hinzuzuziehen. King (1992) schlägt beispielsweise vor, Wissen mit Frageanfängen wie „Was ist/sind …“ zu erfragen, während zur Überprüfung der Verstehens- und Anwendungsdimension Fragestämme wie „Was ist die Hauptaussage von …“ und „Wie würden Sie vorgehen, um …“ genutzt werden können.

Häufig wird empfohlen, den Fragestamm so zu formulieren, dass er auch ohne Antwortoptionen als offene Frage eingesetzt werden könnte (Brauns & Schubert, 2008). Wie die oben abgebildeten Beispiele für Aufgaben im Antwort-Wahl-Verfahren zeigen, ist diese Regel zwar grundsätzlich wertvoll, jedoch nicht immer sinnvoll umsetzbar.

Bei der Erstellung der Antworten stellt besonders das Generieren von geeigneten Distraktoren eine Herausforderung dar. Grundsätzlich gilt: „Ein Distraktor ist dann geeignet, wenn er Personen ohne erforderliches Wissen plausibel erscheint, von Personen mit erforderlichen Fähigkeiten und Kenntnissen jedoch als falsch erkannt wird“ (Lindner et al., 2015, S. 137). Bei der Neukonstruktion von Aufgaben ist es hilfreich, sich an typischen Fallstricken oder Fehlvorstellungen der Studierenden zu orientieren (ebenda). Liegen bereits alte Klausuren mit offenem Antwortformat vor, können diese genutzt werden, um solche Schwachstellen zu identifizieren (Brauns & Schubert, 2008).

Gute Antwortoptionen – sowohl Distraktoren als auch richtige Antworten – zeichnen sich dadurch aus, dass sie annähernd gleich lang sind, eine inhaltliche Homogenität und Gleichwertigkeit bezüglich Thema, Fachsprache und Detaillierungsgrad aufweisen, aber dennoch voneinander unabhängig sind (Brauns & Schubert, 2008). Formulierungen wie „nie“, „immer“ oder „vollkommen“ in Falschantworten oder die Wiederholung einer Formulierung aus dem Fragestamm in der richtigen Antwort können unerwünschte Lösungshinweise geben. Solche oder andere Hinweise entdeckt man am besten, wenn man die Antwortalternativen ohne den Fragestamm präsentiert und von einer dritten Person beurteilen lässt (ebenda).

Bei einer gelungenen Fragenkonstruktion sollte jeder Distraktor von mindestens 5% der Personen gewählt werden (Lindner et al., 2015). Dies kann im Rahmen der Klausurevaluation mit Hilfe einer quantitativen Aufgabenanalyse überprüft werden, die weiter unten dargestellt ist. Oftmals ist es jedoch nicht möglich, mehr als drei oder vier plausible Antworten zu finden (ebenda). Bietet man dennoch zusätzliche Distraktoren von schlechter Qualität an, werden diese häufig unmittelbar als falsch identifiziert und als Antwortalternative ausgeschlossen. In der Konsequenz verlängert sich lediglich die Lesezeit, während die intendierte Erhöhung der Ratewahrscheinlichkeit ausbleibt. Daher gilt die Regel, dass die Distraktorqualität Vorrang vor der Distraktorquantität hat und im Zweifelsfall lieber die Aufgaben- als die Distraktorzahl erhöht werden sollte (ebenda).

Zu guter Letzt wird eine Gleichverteilung aller Antwortalternativen in der Klausur und ihre zufällige Verteilung über alle Aufgaben empfohlen (Brauns & Schubert, 2008). Es sollte also vermieden werden, dass beispielsweise die richtige Antwort immer an dritter Stelle steht.

Zur Evaluation einer Klausur im Antwort-Wahl-Verfahren empfiehlt sich eine Aufgabenanalyse, bei der die Eigenschaften der konstruierten Fragen im Anschluss an die Prüfung bestimmt werden. Hieran wird ersichtlich, ob alle Distraktoren hinreichend häufig genutzt wurden oder ob eine Frage im Antwort-Wahl-Verfahren, die als schwer zu lösende Aufgabe konzipiert wurde, tatsächlich den intendierten Schwierigkeitsgrad besitzt. Damit dient die Aufgabenanalyse der Überprüfung der eigenen Kompetenz beim Entwickeln von Aufgaben (Sacher, 2014, Kap. 6). Sie erlaubt aber auch tiefere Einblicke in das Bearbeitungs- und Lösungsverhalten der Studierenden und stellt dadurch besonders im Rahmen von Zwischenprüfungen eine Hilfe zur Einleitung unterrichtlicher Maßnahmen dar (ebenda). Am Ende einer Veranstaltung liefert sie Hinweise auf typische Schwierigkeiten, denen dann im darauffolgenden Semester an einer neuen Kohorte vorgebeugt werden kann. Zudem ist das Erstellen eines bewährten Aufgabenrepertoires für zukünftige Prüfungen sinnvoll. So können bei der Klausurkonzeption Aufgaben überarbeitet oder Fragen mit einem bestimmten Schwierigkeitsgrad gezielt eingesetzt werden.

Für die Durchführung einer Aufgabenanalyse werden weder avancierte statistische Kenntnisse noch eine besondere Software benötigt; sie lässt sich einfach und unkompliziert mit einem herkömmlichen Tabellenkalkulationsprogramm (z.B. in MS Excel) durchführen. Es empfiehlt sich, bei der Erstellung der Datenmaske eine hohe Sorgfalt an den Tag zu legen und direkt Formeln einzuprogrammieren. Über Letztere lassen sich die Daten schnell auswerten und anschauliche Grafiken erstellen (Franze & Zastrau, 2016), sodass im nächsten Semester lediglich eine neue Dateneingabe erfolgen muss und das Auswertungsprozedere weitestgehend automatisiert erfolgt.

Führt man statt einer klassischen Paper-Pencil-Klausur eine Scan-Klausur (siehe oben) oder sogar eine E-Prüfung durch, so muss man sich gar nicht um die Erstellung einer Aufgabenanalyse kümmern. Diese erfolgt automatisch durch die Prüfungssoftware.

In Abbildung 5 ist der Aufbau einer Datenmaske in MS Excel exemplarisch für eine Prüfung im Antwort-Wahl-Verfahren mit n Klausuren dargestellt, die sechs Single-Choice-Aufgaben mit jeweils vier Antwortalternativen umfasst. Die Daten von n = 10 Klausuren wurden bereits eingetragen, wobei die Ergebnisse einer jeden Person in einer Zeile des Datenblatts stehen. Nur die Werte in den Spalten B–H müssen manuell eingegeben werden, die anderen Angaben können in MS Excel automatisch über Formeln errechnet werden.

Bei Betrachtung der Datenmaske fällt auf, dass die einzelnen Spalten in der ersten Zeile beschriftet wurden:

• In Spalte A werden die Klausurteilnehmer/-innen mit einer laufenden Nummer (1 bis n) versehen.
• In den Spalten B–G wurden die Ergebnisse der Studierenden eingetragen. Hierbei handelt es sich um diejenigen Antwortalternativen, welche für die einzelnen Aufgaben angekreuzt wurden.
• In Spalte H wird die im Rahmen der Klausurauswertung manuell errechnete Gesamtpunktzahl eingetragen.
• In den Spalten I–N werden aus den Angaben in den Spalten B–G über eine „WENN“-Funktion automatisch die von den Studierenden erreichten Punkte ausgerechnet. Wurde die richtige Antwortalternative gewählt, wird eine Eins errechnet; wurde ein Distraktor angekreuzt, erscheint eine Null.
• In Spalte O wird erneut die Gesamtpunktzahl errechnet, nun aber automatisiert über die „SUMME“-Funktion in Excel. Dies dient der Kontrolle der manuellen Rechnung.
• In Spalte P erfolgt ein Abgleich der manuell errechneten Gesamtpunktzahl (Spalte H) mit der über die Summenformel errechneten Gesamtpunktzahl (Spalte O) über die „WAHR“-Funktion.

Eine so vorbereitete Excel-Maske bietet eine solide Grundlage für die weitere Datenauswertung.

Die wichtigsten Kennwerte der quantitativen Aufgabenanalyse sind die Nutzungshäufigkeit der Antwortalternativen, die Aufgabenschwierigkeit und die Trennschärfe. Die Nutzungshäufigkeit überprüft man am besten graphisch, indem man für jede der Aufgaben ein Balkendiagramm erstellt, in dem die Häufigkeitsverteilung der Antwortalternativen dargestellt ist. Wie bereits beschrieben gilt die Faustregel, dass jeder Distraktor von mindestens 5% der Personen angekreuzt worden sein sollte (Lindner et al., 2015). Wird ein Distraktor seltener oder gar nicht genutzt, ist er sehr leicht als Falschantwort zu identifizieren. Im Rahmen der Fragenüberarbeitung sollte ein solcher Distraktor entweder umformuliert, ausgetauscht oder ganz entfernt werden.

Üblicherweise bestanden bereits im Rahmen der Klausurkonzeption Vermutungen über die Schwierigkeit der einzelnen Aufgaben. Um diese Annahmen zu überprüfen, kann die Aufgabenschwierigkeit (oftmals auch als Lösungsanteil oder Lösungsprozent bezeichnet; vgl. Ingenkamp & Lissmann, 2008, S. 162; Sacher, 2014, S. 132f) berechnet werden. Ihre Berechnung erfolgt über Bestimmung des prozentualen Anteils der gelösten Aufgaben am Anteil aller bearbeiteten Aufgaben:

Der Lösungsanteil drückt aus, wieviel Prozent der Studierenden eine Aufgabe korrekt gelöst haben und kann Werte zwischen 100 (minimale Schwierigkeit) und 0 (maximale Schwierigkeit) annehmen. Aufgaben, die nur von wenigen Studierenden gelöst werden (LA ≤ 20%), gelten als schwierig, während Aufgaben, die von vielen Studierenden (LA ≥ 80%) gelöst werden, leicht sind (Ingenkamp & Lissmann, 2008, S. 162; Sacher, 2014, S. 132–134).

Zur Veranschaulichung: In unserem Beispiel in Abbildung 5 haben acht von zehn Studierende Aufgabe 2 korrekt gelöst. Dies entspricht einem Lösungsanteil von 80%. Es handelt sich um eine leichte Aufgabe.

Damit das gesamte Leistungsspektrum erfasst werden kann, sollten in einer Klausur Aufgaben aller Schwierigkeitsstufen vorhanden sein. Idealerweise sind mittelschwere Aufgaben stärker vertreten als leichte und schwere Aufgaben, damit der Test im mittleren Fähigkeitsbereich, der den Regelfall darstellt, eine höhere Diskriminationsfähigkeit besitzt als in den (eher selten vorkommenden) Randbereichen (Sacher, 2014).

Die Trennschärfe einer Aufgabe ist ein Indikator für deren Validität , die Gültigkeit der Messung. Sie gibt an, inwieweit das Gesamtergebnis der Prüfung durch die einzelne Aufgabe repräsentiert wird (Ingenkamp & Lissmann, 2008, 1262-163; Sacher, 2014, S. 134–137). Misst eine Aufgabe dieselbe Fähigkeit wie die restlichen Aufgaben, sollten Studierende, die im Test eine hohe Gesamtpunktzahl erzielen, die einzelne Aufgabe mit einer höheren Wahrscheinlichkeit lösen als Studierende mit einem schlechten Klausurergebnis. Eine Berechnung der Trennschärfe erfolgt über die Formel

Wichtig ist, dass die Bestimmung der besseren bzw. der schlechteren Hälfte der Studierenden über die in der Klausur erreichte Gesamtpunktzahl bestimmt wird, als „erreichte Punkte“ im Zähler jedoch die Punkte in der einzelnen Aufgabe, für welche die Trennschärfe berechnet werden soll, in die Formel eingesetzt werden. Um die Trennschärfe von Aufgabe 2 in Abbildung 5 zu berechnen, muss daher im ersten Schritt die erreichte Gesamtpunktzahl (Spalte O) betrachtet werden. Hier zeigt sich, dass die Studierenden mit den Teilnehmernummern 1, 3, 7, 9 und 10 die bessere Hälfte und die Studierenden mit den Teilnehmernummer 2, 4, 5, 6 und 8 die schlechtere Hälfte bilden. Ein Blick in Spalte J verrät, dass alle fünf Studierenden der besseren Hälfte Aufgabe 2 lösen konnten, während dies nur drei der fünf Studierenden der schlechteren Hälfte gelungen ist. Es resultiert:

Die Interpretation dieses Ergebnisses darf nicht unabhängig von der Aufgabenschwierigkeit erfolgen. Sacher (vgl. Sacher, 2014) empfiehlt:

• „Sofern der Lösungsanteil der analysierten Aufgabe zwischen 20 und 80 liegt, sollte die […] Tr mindestens 20, besser aber 33 betragen“ (S. 136).
• „Bei Aufgaben mit einem Lösungsanteil über 80 genügt auch eine Trennschärfe von mindestens 10, besser aber 17“ (S. 137).

Alles in allem ist die Trennschärfe von Aufgabe 2 als gut zu bewerten. Diese Aufgabe scheint etwas Ähnliches zu messen wie die anderen Klausurfragen und passt daher gut in die Klausur.

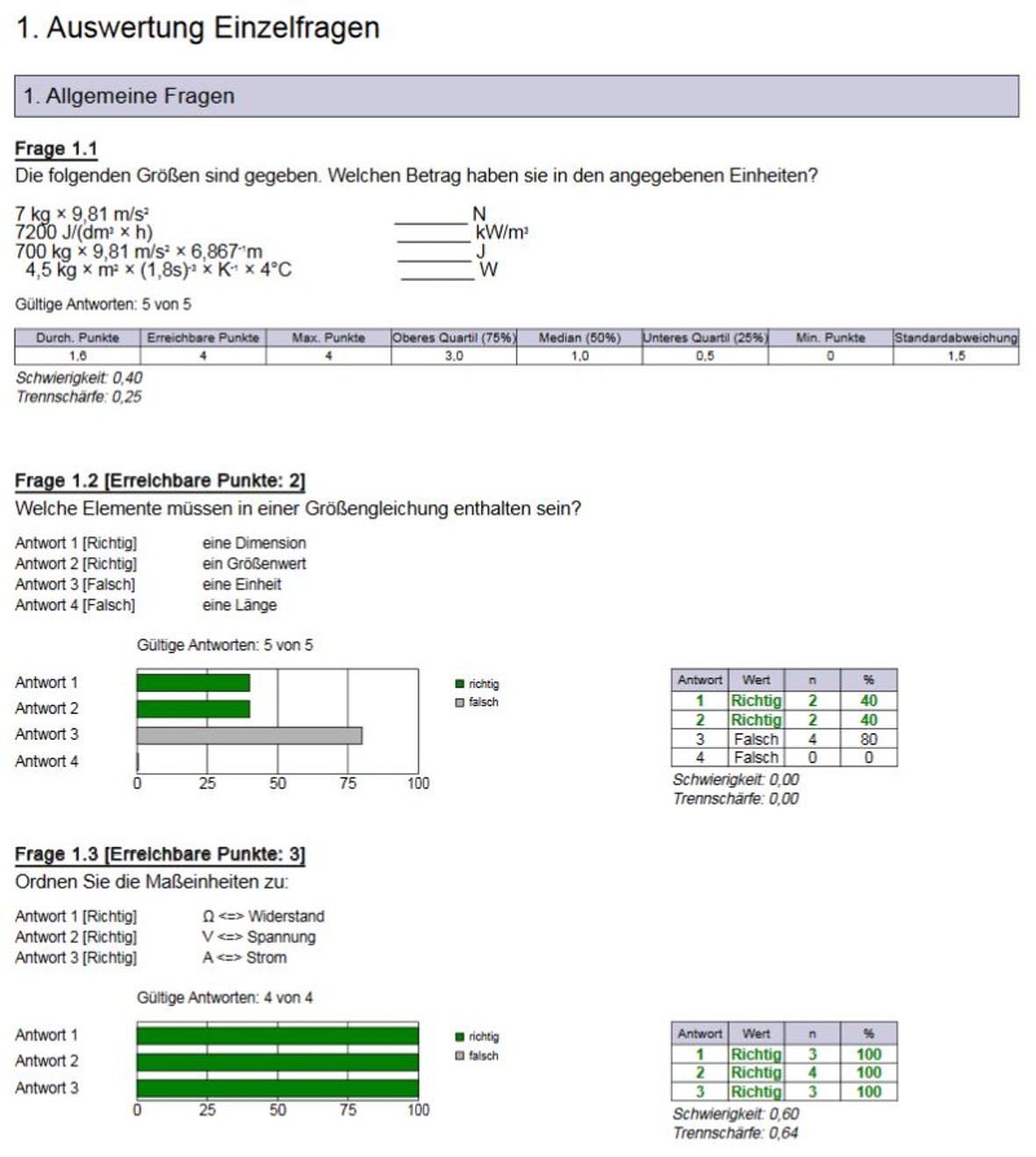
Bei einer Scan-Klausur oder auch E-Prüfung werden die Aufgabenschwierigkeit und Trennschärfe automatisch auf Grundlage der Auswertungsdaten vom Prüfungssystem berechnet und i.d.R. im Rahmen eines Reports (siehe Abbildung 6) dargestellt. Dieser enthält ebenso die Distraktoren-Analyse, die für jede Aufgabe als Balkendiagramm aufbereitet ist.

Abschließend ist darauf hinzuweisen, dass man sich bei der Interpretation der Ergebnisse einer quantitativen Aufgabenanalyse niemals dogmatisch an den oben genannten Cut-Off-Werten orientieren sollte. Vielmehr sollte die Interpretation dieser Kennwerte vor dem Hintergrund einer qualitativen Analyse erfolgen, in deren Rahmen bei der Bewertung der Aufgabenqualität auch die Frageinhalte berücksichtigt werden. Hierzu nimmt man am besten die Klausur erneut zur Hand und markiert alle Auffälligkeiten: Distraktoren, die nicht gewählt wurden, Fragen mit unerwartet hohen oder niedrigen Schwierigkeiten oder geringen Trennschärfen. Beispielsweise könnte sich zeigen, dass in einer Klausur nur sehr wenige schwere, aber ungefähr gleich häufig mittelschwere und leichte Aufgaben vorkommen. Dies widerspricht auf den ersten Blick den oben genannten Empfehlungen zur Testkonstruktion und könnte Lehrende in Versuchung führen, den Schwierigkeitsgrad der Aufgaben im kommenden Semester zu erhöhen. Wurde die Klausur jedoch unter Berücksichtigung des Constructive Alignments (Biggs & Tang, 2011) sorgfältig konstruiert, können diese Ergebnisse auch darauf hinweisen, dass ein Großteil der Studierenden die Lernziele erreicht hat. Das abschließende Urteil darüber, ob die Klausur insgesamt zu leicht oder zu schwer war, liegt daher immer im Ermessen des Lehrenden.

Sacher, W. (2014). Leistungen entwickeln, überprüfen und beurteilen. Bewährte und neue Wege für die Primar- und Sekundarstufe (6., überarb. und erw. Aufl). Bad Heilbrunn: Klinkhardt.

King, A. (1992). Facilitating Elaborative Learning Through Guided Student-Generated Questioning. Educational Psychologist, 27 (1), 111–126.

Ingenkamp, K. & Lissmann, U. (2008). Lehrbuch der pädagogischen Diagnostik (6. Aufl.). Weinheim: Beltz.

Franze, A. & Zastrau, B. W. (2016). Mehr als ein Kuchendiagramm – Möglichkeiten der Prüfungsauswertung. HDS.Journal, 1/2016, 34–38. Zugriff am 18.08.2016. Verfügbar unter http://ul.qucosa.de/fileadmin/data/qucosa/documents/20260/hds_jounal_I_2016-2.pdf

Biggs, J. B. & Tang, C. S.-k. (2011). Teaching for quality learning at university. What the student does (4th ed.). Maidenhead: McGraw-Hill.

Lindner, M. A., Strobel, B. & Köller, O. (2015). Multiple-Choice-Prüfungen an Hochschulen? Zeitschrift für Pädagogische Psychologie, 29 (3-4), 133–149.

Brauns, K. & Schubert, S. (2008). Qualitätssicherung von Multiple-Choice-Prüfungen. In S. Dany, B. Szczyrba & J. Wildt (Hrsg.), Prüfungen auf die Agenda! Hochschuldidaktische Perspektiven auf Reformen im Prüfungswesen (1. Aufl., S. 93–102). Bielefeld: Bertelsmann.

Anderson, L. W. & Krathwohl, D. R. (2001). A taxonomy for learning, teaching, and assessing. A revision of Bloom's taxonomy of educational objectives. New York: Longman.