Techniken für gute Prüfungsaufgaben in Klausuren
31.03.2022
Beim Erstellen von Prüfungsaufgaben die Ziele der Lehrveranstaltung einzubeziehen, ist eine machbare Herausforderung.
Mit der Öffnung einer Aufgabe ist die Transformation einer Aufgabe mit geschlossenem Antwortformat in eine Aufgabe mit offenem Antwortformat gemeint. Zu diesem Zweck können Sie sich bei der Aufgabenstellung zum Beispiel an einem Ergebnis orientieren. Sie geben dann keine Ausgangswerte mehr vor und fragen nach dem Endergebnis, sondern lassen Ihre Studierenden ausgehend von einem Ergebnis auf die Ausgangsbedingungen rückschließen.
Das folgende Beispiel soll Ihnen die Idee der Öffnung einer Aufgabe näherbringen. Die ursprüngliche Aufgabe lautet wie folgt:
„Zeichne ein Parallelogramm, dessen Grundseite 8 cm lang ist und dessen Höhe 3,5 cm lang ist und berechne den Flächeninhalt dieses Parallelogramms.“
Nach dem Öffnen der Aufgabe lautet sie folgendermaßen:
„Zeichne ein Parallelogramm mit einem Flächeninhalt von 24 cm².“
Sie erkennen, dass sich durch Ihre Öffnung auch die Anforderungen der Aufgabe ändern. Aus einer einfachen Reproduktionsaufgabe wird eine Aufgabe, die das Verständnis der Prozedur in Form von Konzeptwissens stärker in den Fokus rückt. Durch die Umkehrung wird die Aufgabe außerdem „robuster“ gegenüber dem einfachen Einüben von Standardrechenschritten.
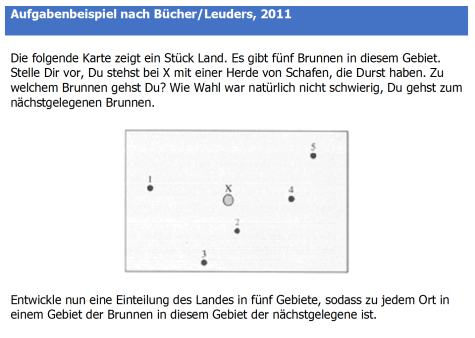
Die folgende Abbildung zeigt das Öffnen von Aufgaben anhand von drei verschiedenen Aufgabenbeispielen:
Die Fähigkeit, Begründungen und Einschätzungen zu einer bestehenden Problemstellung zu geben, erfordern neben einem entsprechenden Basiswissen auch ein prozedurales und konzeptuelles Verständnis über die Vorgänge und Zusammenhänge in Verbindung mit einem fachlichen Konzept. Über einfache „Fakten“ hinaus müssen Ihre Studierenden also auch wissen, wie sich diese Fakten in Prozessen darstellen und wie die einzelnen Wissensbausteine und Prozeduren konzeptuell miteinander verschränkt sind.
Sieht eines Ihrer Lehrziele eine solche Fähigkeit vor, so eignen sich zur Überprüfung zum Beispiel Aufgaben in Form von Aussagen, die von den Studierenden begründet beurteilt werden sollen. Das Kriterium dabei ist also, dass eine solche Beurteilung ohne ein prozedurales und konzeptuelles Wissen nicht möglich ist.
Die folgenden Beispiele von Aufgabenstellungen können Sie als Beispiele dafür verstehen, wie Sie Ihre Studierenden zu Begründungen und Einschätzungen anleiten können. In diesen Beispielen werden dabei mögliche Lösungen vorgegeben, während die richtigen Lösungswege begründet werden sollen.
Auch das Erfragen von Anwendungsbeispielen oder Grenzen ermöglicht es Ihnen, anspruchsvollere Lehrziele, zum Beispiel über das Erlangen konzeptuellen Wissens oder – aber begrenzt – auch die Anwendbarkeit des Gelernten zu überprüfen. Begrenzt deshalb, da es sich hierbei tatsächlich nicht um Anwendungsaufgaben handelt. Die Beschreibung einer Anwendung und die Anwendung selbst unterscheiden sich noch einmal in erheblichem Maße. Sie sollten also auch bei diesen Beispielen beachten, dass auch das Erfragen von Anwendungsbeispielen und Grenzen noch im Bereich eines kompetenzorientierten Wissenstests (Vgl. Grundsätze bei der Erstellung von Prüfungsaufgaben) liegt und somit eher ganz grundsätzliche Voraussetzungen für eine spätere Kompetenz überprüft.
Die folgenden Beispiele zeigen Möglichkeiten bei der Erfragung von Anwendungsbeispielen oder -grenzen.
Beispiel 1:
Gib jeweils einen Wachstumsprozess an, der sich besonders gut durch eine
a) Exponentialfunktion
b) quadratische Funktion
c) lineare Funktion
abbilden lässt.
Um die Aufgabe in Beispiel 1 lösen zu können, müssen Studierende das Konzept des Wachstumsprozesses verstanden haben. Auch muss verstanden worden sein, dass sich reale Phänomene in Form mathematischer Modelle (in diesem Fall bestimmter Funktionen) abbilden lassen.
Beispiel 2:
Noch etwas anspruchsvoller lässt sich die Aufgabe gestalten, indem auch die Grenzen der mathematischen Abbildbarkeit thematisiert werden, wie Aufgabenbeispiel 2 aus SINUS Transfer zeigt.
Gib einen Wachstumsprozess an, der sich weder durch eine Exponentialfunktion, noch durch eine quadratische Funktion, noch durch eine lineare Funktion angemessen beschreiben lässt!
Beispiel 3:
Beispiel 3 aus dem PISA-Test 2006 wiederum zeigt, wie Sie diese Form der Aufgabenstellung mit Bezug auf ganz spezifische Kompetenzen (hier: Diagrammlesekompetenz) gestalten können. Im Beispiel werden mögliche Schlussfolgerungen aus einem Diagramm zur Auswahl gestellt. Die Schülerinnen und Schüler sollten in diesem Fall die Schlussfolgerung wählen, die sich aus der Darstellung begründet ableiten lässt. Diese Aufgabe ist gleichzeitig ein Beispiel dafür, dass auch unter Verwendung des Wahl-Antwort-Formats durchaus anspruchsvolle Aufgabenstellungen möglich sind.
Eine wesentliche Voraussetzung zur Entwicklung von Kompetenzen ist es, dass Studierende zentrale Begriffe einer Domäne kennen und verstehen. Entsprechend gibt es viele Prüfungsaufgaben, in denen Begriffe definiert und erklärt werden sollen. So einfach derartige Aufgaben auf den ersten Blick wirken, ist auch dieser Typus recht vielseitig gestaltbar. Zwei Variationen solcher Aufgaben werden im Folgenden an Beispielen aufgezeigt, die jeweils auf den Begriff „Mittelsenkrechte“ führen. Auch diese Beispiele sind schulischen Vergleichstests entnommen und dementsprechend für Sie als Hochschullehrende inhaltlich natürlich wenig komplex. Das Prinzip hinter der Technik wird aber dadurch besonders deutlich.
Beispiel mit einer geschlossenen Aufgabenstellung:
Zeichne eine Strecke AB. Schlage dann einen Kreis um A und einen Kreis mit demselben Radius um B, so dass sich beide Kreise schneiden. Verbinde die Schnittpunkte. Welche Eigenschaft weißt die entstehende Gerade auf?
Als Abschluss der Aufgabe sollte der Begriff der „Mittelsenkrechten“ genannt werden. Dabei gibt es nur eine richtige Lösung, die Studierenden werden also durch die Aufgabenstellung eng geführt. Die Aufgabe sieht dabei eine bestimmte Prozedur vor, die aber nicht im Fokus der Aufgabe steht und deshalb mit vorgegeben wird. Verstanden werden muss zur korrekten Darstellung lediglich der Begriff des Radius sowie die Konzepte der Schnittpunkte und der Geraden. Durch die geschickte Hinführung auf die eigentliche Fragestellung („Welche Eigenschaft weist die entstehende Gerade auf?“) wirkt die Aufgabe jedoch aktivierend.
Das folgende Beispiel zeigt dagegen eine Aufgabe, die auf demselben inhaltlichen Konzept, jedoch eine offene Aufgabenstellung enthält:
Der gesuchte Begriff in hier Teil einer ungleich komplexeren Problemlösungsaufgabe. Die Problemstellung wurde dabei so konstruiert, dass die lösende Person während der Lösung der Aufgabe auf das Prinzip der „Mittesenkrechten“ gestoßen wird. Inwieweit der Begriff dann auch explizit genannt werden muss, ist wiederum eine Frage des dahinterstehenden Lehrziels, je nachdem, ob die Lösungsprozedur stärker oder weniger stark bewertet werden soll. Die Studierenden sollten im Falle solcher Aufgabe jedoch nicht zu sehr dafür „bestraft“ werden, wenn sie den Begriff nicht konkret benennen, aber ein Verständnis für Konzept und Prozedur zeigen. Der spezifische „Reiz“ einer solchen Aufgabenstellung liegt also darin, dass ein bestimmter Begriff bzw. ein bestimmtes Konzept von den Studierenden „entdeckt“ werden muss und sich an einem konkreten Anwendungsfall plausibilisiert.
Literatur
Büchter, A. (2006). Verstehensorientierte Aufgaben als Kern einer neuen Kultur der Leistungsüberprüfung. SINUS-Transfer: Erläuterung zu Modul 10. Online-Publikation. http://sinus-transfer.uni-bayreuth.de/fileadmin/MaterialienDB/427/Buechter_Modul_10.pdf (wird in neuem Tab geöffnet)
Büchter, A. & Leuders, T. (2011). Mathematikaufgaben selbst entwickeln. Lernen fördern – Leistung überprüfen. 5. Auflage. Berlin: Cornelsen Scriptor.
Aufgabenbeispiele
OECD Programme for International Student Assessment (2006): PISA 2006: Beispielaufgaben aus dem Naturwissenschafsttest. Online verfügbar unter:
http://archiv.ipn.uni-kiel.de/PISA/fr_reload.html?home.html
SINUS-Transfer (2015). Materialdatenbank. Online verfügbar unter: http://sinus-transfer.uni-bayreuth.de/materialien/materialdatenbank.html
Vergleichsarbeiten (VERA). Bildungsserver Berlin-Brandenburg. Verfügbar unter:
https://bildungsserver.berlin-brandenburg.de/vera